Pourquoi ce qu’on a fait hier c’est tout pourri

On va prendre une équation différentielle simple, dont on connait la solution analytique. L’équation la plus simple qui me vient à l’esprit au moment où j’écris ces lignes c’est :

$$ \begin{equation} y^\prime(t) = \cos(t) \label{eq} \end{equation}$$

C’est simple parce que sa solution est… $y(t) = \sin(t) + \text{constant}$. [0] Du coup, ce que je vous propose c’est de calculer la solution de cette équation avec la méthode d’Euler et de comparer avec le résultat analytique. Normalement, vu la simplicité de l’équation, vous devriez trouver le code pour faire la méthode d’Euler tout seul ^^ (je vous laisse faire hein !)

La figure ci-dessous montre la courbe de la solution analytique (en vert) et celle obtenue par la méthode d’Euler (en bleue) (avec $dt = 0.1$, pour $t \in [0, 10[$). (Vous pouvez cliquer pour agrandir)

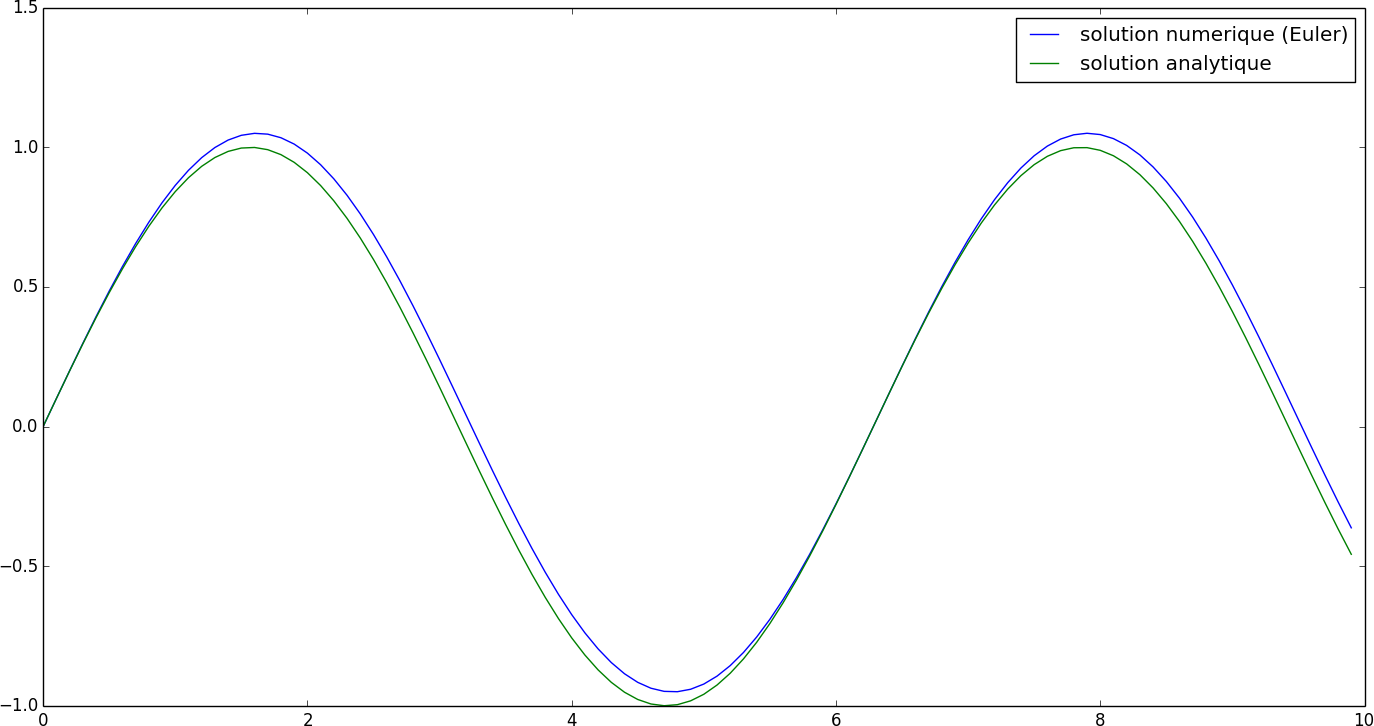
Vous voyez comment on dévie de la solution ? Bref, il faut faire autrement :p

Tada… la méthode de Runge-Kutta

Je vous propose de vous balancer la méthode à la figure, on la programme bêtement, on regarde si effectivement ça vaut le coup (ou si je vous ai dit des âneries). Ça vous va ? (j’espère que oui parce qu’on y va…)

On commence par la méthode dite « RK4 ». Ça consiste à calculer quatre quantités $k_i$, puis à les utiliser pour calculer la valeur de $y$ à l’instant $t_n$ voulu. Voyez plutôt.

On a $y^\prime(t) = f(y, t)$ et on se donne $y(t = 0) = y_0$. À l’instant $t_n$, on calcule alors nos $k_i$ comme suit :

$$ \begin{cases} k_1 = f(y_n, t_n)\newline k_2 = f(y_n + \frac{dt}{2}k_1, t_n + \frac{dt}{2})\newline k_3 = f(y_n + \frac{dt}{2}k_2, t_n + \frac{dt}{2})\newline k_4 = f(y_n + k_3, t_n + dt) \end{cases} $$

puis pour calculer la valeur de $y$ à l’instant $t_{n+1}$, on les assemble ainsi :

$$ y_{n+1} = y_n + \frac{dt}{6}\left(k_1 + 2k_2 + 2k_3 + k_4\right) $$

Ainsi par réccurence, comme avec la méthode d’Euler, on peut calculer $y_{n+1}$ à partir de $y_n$.

Voyons ce que ça donne en python sur la même équation qu’avant $\eqref{eq}$.

Comme d’habitude, on définit l’espace temporel, la fonction qui nous donne la dérivée, etc… D’ailleurs, à partir de maintenant cette fonction on va l’appeller rhs() pour Right Hand Side, c’est la convention…

>>> from pylab import *
>>> tf = 10 #on simule 10 secondes…
>>> dt = 0.1
>>> times = arange(0, tf, dt)
>>> def rhs(y, t):
...     return sin(t)
>>>

On fait donc une fonction qu’on va appeller rk45() qui va prendre en paramètre l’espace temporel, la fonction rhs() et notre condition initiale. Et en retour, cette fonction nous donne la solution sur l’espace temporel considéré. C’est une implémentation assez directe de ce que j’ai donné au dessus.

>>> def rk45(y0, dt, times, rhs):
...     y = array(y0)
...     solutions = [] #on va stocker les valeurs calculées ici
...     for t in times:
...         solutions.append(y)
...         k1 = rhs(y, t)
...         k2 = rhs(y + dt/2.0*k1, t + dt/2.0)
...         k3 = rhs(y + dt/2.0*k2, t + dt/2.0)
...         k4 = rhs(y + k3, t + dt)
...         y = y + dt/6.0*(k1 + 2*k2 + 2*k2 + k3)
...     return array(solution)
>>>

Il ne nous reste plus qu’à appeller cette fonction sur nos valeurs et à comparer avec la solution exacte pour voir si on fait mieux qu’avec Euler…

>>> ycomputed = rk45(0.0, dt, times, rhs)
>>> plot(times, ycomputed, label='solution numerique (RK4)')
>>> plot(times, cos(times), label='solution analytique')
>>> legend()
>>> show()

Et normalement, vous devriez voir ça : (soit deux courbes hyper bien superposées !)

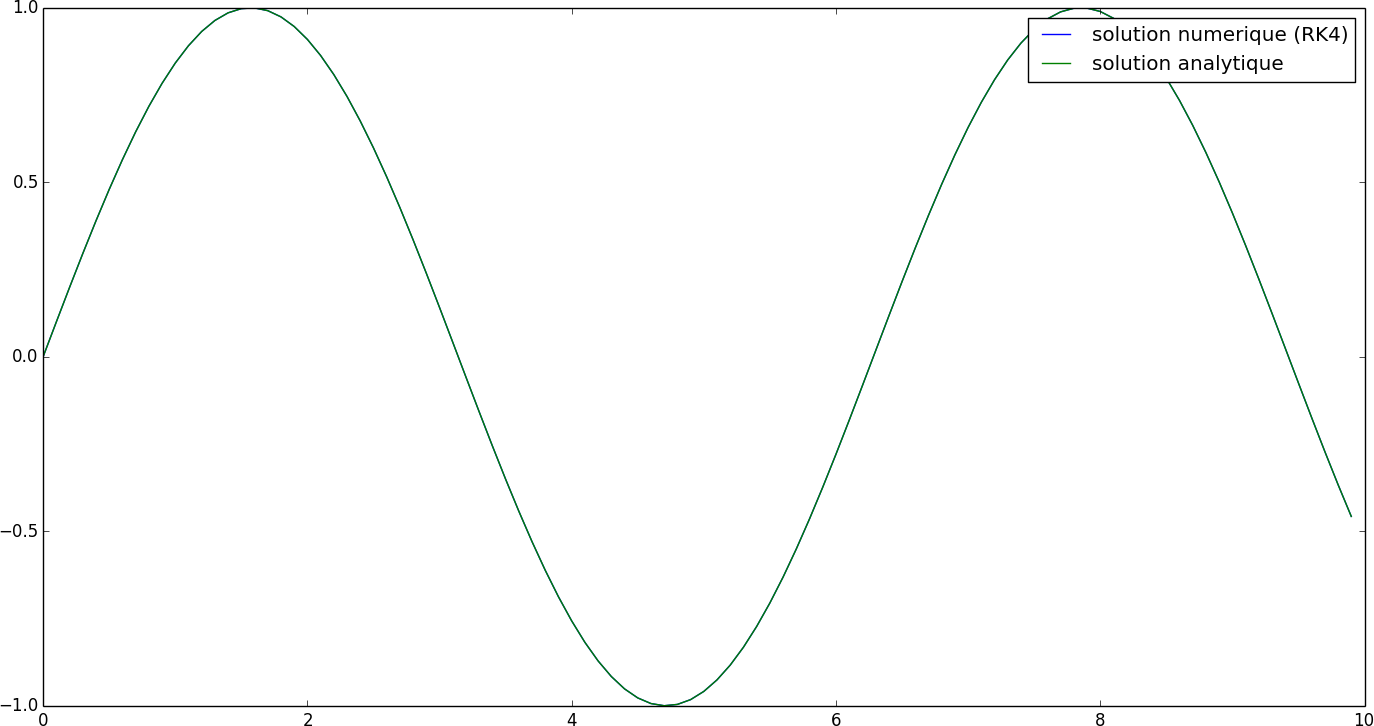
Alors, c’est pas mal hein ? Pour information, avec la méthode d’Euler et un pas de temps de $dt = 0.1$, je trouve une erreur cumulée d’environ $5.21$. Avec la méthode RK4, pour le même pas de temps, je trouve une erreur cumulée d’environ $2.13\times 10^{-6}$. Je crois que c’est assez parlant…

Moralité ? Et bien… ça vaut le coup d’utiliser cette méthode, non ?

Cas général

Je vous ai parlé de la méthode RK4. Comme vous vous en êtes sans doute doutés, si celle-ci a un nom… c’est que y en a d’autres. Il en existe plein la littérature des méthodes du Runge-Kutta en fait. Donc, on va donner ici la formulation générale.

Dans le cas génénal, on calcule $y_{n+1}$ comme ça :

$$ y_{n+1} = y_n + dt\sum_{i = 1}^{s} b_ik_i $$

où les $k_i$ sont calculés ainsi :

$$\begin{cases} k_1 &= f(y_n, t_n)\newline k_2 &= f(y_n + dt a_{21} k_1, t_n + c_2dt)\newline k_3 &= f(y_n + dt(a_{31} k_1 + a_{32} k_2), t_n + c_3dt)\newline &\vdots\newline k_s &= f(y_n + dt(a_{s1} k_1 + a_{s2} k_2 + … + a_{s,s-1}k_{s-1}), t_n + c_sdt) \end{cases} $$

Et donc avec cette notation, il suffit juste de donner les valeurs de tous les $b_i$, de tous les $c_i$ et de tous les $a_{ij}$ pour définir une méthode de Runge-Kutta particulière. Il est courant de donner ces valeurs sous la forme d’un tableau, appelé tableau de Butcher :

$$ \begin{array}{c|*{6}{c}} 0 & & & & & \newline c_2 & a_{21} & & & & \newline c_3 & a_{31} & a_{32} & & & \newline \vdots & \vdots & & \ddots & & \newline c_s & a_{s1} & a_{s2} & \cdots & a_{s,s-1} & \newline \hline & b_1 & b_2 & \cdots & b_{s-1} & b_s \end{array} $$

Maintenant que vous savez ça, je peux vous donner le tableau de Butcher de RK4 :

$$ \begin{array}{c|*{4}{c}} 0.0 & & & & \newline 0.5 & 0.5 & & & \newline 0.5 & 0.0 & 0.5 & & \newline 1.0 & 0.0 & 0.0 & 1.0 & \newline \hline & \frac{1}{6} & \frac{1}{3} & \frac{1}{3} & \frac{1}{6} \end{array} $$

D’ailleurs, je vous ai dit hier que la méthode d’Euler n’était qu’un cas particulier des méthodes de Runge-Kutta… Elle peut donc être résumée à un tableau de Butcher et le voici :

$$ \begin{array}{c|c} 0.0 & 0.0 \newline \hline & 1.0 \end{array} $$

Normalement, il n’y a plus qu’à vous donner un tableau de Butcher, et vous savez programmer la méthode correspondante. N’est-ce pas ? :D

Vous trouverez une petite liste sur cette page.

Conclusion

Nous avons donc vu ce que sont les méthodes de Runge-Kutta. On a vu un exemple, la méthode RK4. Ce que je vous invite à faire maintenant, c’est d’intégrer le code de cette méthode à ce qu’on a fait hier avec le caillou qu’on jettait en l’air. Vous pourrez ainsi comparer Euler et RK4 et voir si y’a des différences.

Quoi d’autre pour les prochains articles ? Je pense que la prochaine fois, je vous parlerai de la transformée de Fourier discrète. Je vous parlerai de ça et ça me permettra ainsi d’aborder les méthodes pseudo-spectrales, qui nous permettrons ensuite d’aborder la résolution de certaines équations aux dérivées partielles dans le cas périodique (comme l’équation des ondes). Et puis, on pourra peut être enfin parler de vagues… Comme vous le voyez, la route est encore longue. J’espère que vous êtes toujours motivés ;)

Le moment venu, on parlera aussi de Runge-Kutta imbriqués, de pas de temps adaptatifs, de dense output, etc… Et quand on aura compris tout ça, on pourra jetter un œil à ce que scipy nous propose. Mais plus tard !